性能模型（Amdahl&Little’s Law）

Amdahl’s Law

提升一个系统的一个部分的性能对整个系统有多大影响？

  • 当提升系统的一部分性能时，对整个系统性能的 影响取决于:
    – 1、这一部分有多重要
    – 2、这一部分性能提升了多少

·对于一个计算中占总时间比为ff的一部分而言， 将该部分的性能提升 s 倍，整个计算的总体性能提升为

\operatorname{Speedup}(f,s)&=\frac1{(1-f)+\frac fs} \\&=\frac1{1-f(1-\frac {1}{s})} \\&=\frac{s}{s+(1-s)f}

· 这里 Speedup(f,s)(f,s) 被称为加速比

Everyone knows Amdahl’s law, but quickly forgets it.

​ —Thomas Puzak, IBM, 2007

在多核计算机的并行场景下，s 可以看作并行处 理器的数量，因此 Amdahl’s Law 给出了并行 程序中处理器数、程序可并发部分占比和加速比 的关系。

提升加速比的方法 :

因此，同时提升可优化程序( 并发程序 ) 占比 f 和性能提升倍率 ( 并发量 ) s 可以提升加速比。这也与直观印象相符。

  • 当f=0.6,s=2时，speedup=10.4+0.62=1.42= \frac 1{0.4+ \frac {0.6}2}= 1.42

  • 当f=0.6\mathrm{f= 0.6} , s=10时，speedup = 10.4+0.610=2.17\frac{1}{0.4+\frac{0.6}{10}}=2.17

  • 当f=0.99,s=10时，speedup=10.01+0.9910=9.17= \frac 1{0.01+ \frac {0.99}{10}}= 9.17

  • 一般来说，如果应用程序有 α 的比例必须串行运行，那 么加速比最多为 1/α

并行场景下的问题

  • 速度提升的最大值受制于串行部分: 串行瓶颈

  • 并行部分也常常并非完美并行
    同步开销(e.g.，更新共享区数据)
    负载不平衡开销(不完美的并行)
    资源共享开销(S个处理器间的竞争)

串行瓶颈

并行机器有串行瓶颈

主要原因: 数据的非并行操作 (e.g. 不可并行的循环)

其他原因: – 由单个线程准备数据并发出并行任 务（通常是串行的

·期望的状态:
·在串行代码区间→一个高性能的“大”核
·在并行代码区间→许多较低性能的“小”核

并行瓶颈

  1. 同步： 对共享数据的操作不能被并行化
    • 锁、互斥、阻塞同步-
    • 通信： 进程间需要相互共享一些数据
    • 共享数据引发竞争时，线程会被序列化
  • 共享数据引发竞争时，线程会被序列化

  1. 负载不平衡： 并行事务存在不同的持续时间

    • 由于不完善的并行化或微架构的影响
    • 降低了并行部分的速度提升

  2. 资源竞争： 并行任务可能共享硬件资源 ,相互造成延迟

    • 复制所有资源 (e.g., 内存) 开销巨大

    • 每个任务单独运行时不存在的额外延迟

  • 并行部分的瓶颈: 另一个角度

  1. 多线程应用程序中的线程可以是相互依赖的- 相对于来自不同应用程序的线程
  2. 这样的线程可以相互同步- 锁,阻塞,pipeline,条件变量,信号量,
  3. 一些线程可能由于同步而处于执行的关键路径上;另一些线程则不是
  4. 即使在一个线程中，有些“代码段”可能在执行的关键路径上;有些则不是
  • 需要注意
    1. 临界区
    2. 阻塞
    3. 流水线程序的阶段

排队模型及其分布

定义

一种信息源模型，特征是由输入、排队、服务三 个过程组成

  1. 输入过程

    • 请求总体:有限、无限
    • 请求到达方式:逐个、成批
    • 请求间隔:确定型、随机型
    • 请求之间的关系:相关的、独立的

  2. 排队规则
    损失制
    等待制
    混合制

  3. 服务规则

    • 多窗口、单窗口

    • 服务时间: 确定型、随机型

运行指标 和分类

  • 系统吞吐率：平均单位时间内被服务完的请求数量

  • 请求响应时间：请求在系统内的平均逗留时间

  • 系统利用率：服务连续繁忙的时间长度

分类和记号

  • X/Y/Z/m (或o,可省略 )来表示排队模型

    X:请求相继到达系统的间隔时间T的概率分布。
    Y:服务所耗费的服务时间 的概率分布
    Z: 系统内服务的个数;
    m : 系统内( 最大)排队容量 ;

  • M/M/n -
    请求到达系统时间间隔与服务时间均服从负指数，系
    统内设有n个服务窗口，
    系统容量为无限的等待制排队模型

泊松流

  • 泊松( Poisson )流，又称最简单事件流。
    其具有如下特点:

    1. 平稳性: 出现任意数量事件的概率只与时间区间t的大小有关，与t的位置无关

    2. 无后效性: 在互不相交的两个时间区间T1、T2内所出现的事件数是相互独立的

    3. 普通性:在同一瞬间多于一个事件出现的概率可忽略不计

      pn(t)=(λt)nn!e−λtp_n(t)=\frac{(\lambda t)^n}{n!}e^{-\lambda t}

  • 用户请求到来的事件流通常符合泊松分布

负指数分布

  • 当请求流为泊松流时,两个相继请求到达系统的 时间间隔 t 分布为:

F(t)=1−e−λtf(t)=λe−λtF(t)=P(T≤t)=1−P0(t)=1−e−λt\begin{aligned} F(t)&=1-e^{-\lambda t} &f(t)&=\lambda e^{-\lambda t} \\\\ F(t)&=P(T\leq t)=1-P_0(t)=1-e^{-\lambda t} \end{aligned}

  • 用 μ 表示单位时间内完成服务响应的事件均值, 则

F(t)=1−e−μtf(t)=μe−μt\begin{aligned} F(t)&=1-e^{-\mu t}\\f(t)&=\mu e^{-\mu t} \end{aligned}

Little’s Law

利特尔定律

  • 考虑一个排队系统M/M/1：
    到达系统的请求符 合排队模型，
    按λ-泊松流到达；
    系统响应时间按 μ-负指数分布；
    服务器数量为1

  • 如何得知系统中停留的请求的平均数量?

在一个系统的长期稳定状态下，系统中负载的平均数量L是平均到达率入和负载在系统中停留的
平均时间W的乘积，即

L=λ×WL=\lambda\times\mathbb{W}

乍一看，利特尔定律看起来像是常识.
然而，这个规律在两个方面很有见地。
首先，它不依赖于任何变量的概率分布。
第二，由于到达率通常小于最大处理率，这个定律给出了系统设计中处理能力必须是多少
如果负载到达的速度超过了系统处理它们的最大速度，系统就会溢出。

Little 模型

对事务和负载到来时的规模采样、对处理时间 样，即可通过Little’s Law算出系统当前的负载量

举例

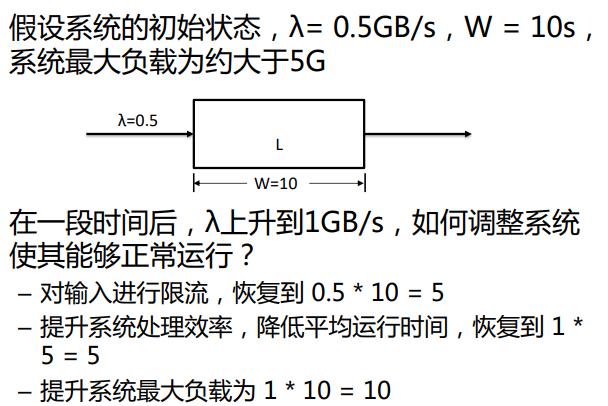
image-20231113204721614

  1. 依据Little’s Law，我们可以得出在事务处理系统和流处理系统中的三个重要指标∶负载流量、处理时间、负载最大容量
  2. 使系统处于可靠状态，就需要将这三个指标保持在正常范围
  3. 如果系统遇到突发情况，需要调整相应指标以维持系统正常运行

性能模型 应用：

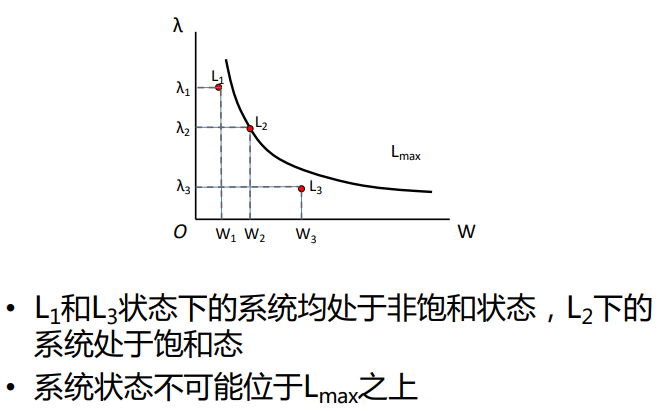
image-20231115171551772

尾延迟

尾延迟分析

  1. 尾延迟 Tail Latency：如果在系统中引入实时监 控，总会有少量响应的延迟高于均值，我们把这 些高延迟称为尾延迟

  2. 尾延迟是影响系统综合性能和服务质量的重要因素

    • 考虑极端情况：系统标准延迟为100ms，有100个响 应，其中99个的延迟为100ms，1个的延迟 为10s

    • 平均延迟为199ms，约为标准延迟的2倍，然而：
      99%的延迟处于正常范围，仅有1%的尾延迟超标
      尾延迟为10s，不仅远远超过标准延迟、影响平均性能，也 给当前用户带来极其糟糕的体验

  3. 最极端的尾延迟─般是由于网络波动、系统抖动等难以解决之情况造成，优化成本过高﹔
    然而，使用平均延迟又难以发现和解决系统处于非极端尾延迟下的情况

  4. 前文回顾︰
    同时提升可优化程序占比f和性能提升倍率s 可以提升加速比
    为什么不能全部优化?代价太高、不可控

如何优化

考虑更一般的情况 M/M/1: 到达系统的请求符合排队模型，按λ-泊松流到达；系统响应时间按μ-负指数分布；服务器数量为1；存在概率极低的偶发异常，会导致响应时间大幅增加

定义系统负载 p 为

ρ=λμ\rho = \frac{\lambda} {\mu}

当p<1p<1时，λ<μ,排队系统稳定；反之，任务不断累积导致不稳定

系统中平均任务数：

E(N)=ρ1−ρE(N)=\frac{\rho}{1-\rho}

平均任务响应时间：

E(R)=E(N)λ−1=1μ−λE(R)=E(N)\lambda^{-1}=\frac{1}{\mu-\lambda}

为了优化服务性能，需要制定一个优化阈值由上推导得，第 p 个百分点的响应时间为

mp=−ln⁡(1−p/100)μ−λm_{\mathfrak{p}}=-\frac{\ln(1-p/100)}{\mu-\lambda}

P99延迟:p取99的情况，即99%的响应所经历的延迟的上限。换句话说，99%的流量所经历的延迟小于P99(又称99分位数99th-
percentile )。
P99延迟是一种尾延迟应用场景，代表系统对99%的延迟予以优化和控制。P99应用最为广泛，除此之外还有P90、P95、P99.9等
为何控制尾延迟只控制P99 ?

P90及更低︰依据Amdahl’ s Law，同样优化倍率s , 90%占比优化相比99%带来的系统总性能提升低
P99.9及更高:保持优化倍率s带来的开销过大，因为存在难以控制的突发状况，如网络波动、系统抖动等
控制P99在合理阈值下，可以兼顾性能和开销

前述M/M/1场景在P99下的 μ - 延迟关系

image-20231113205638429

云计算场景: Serve μs-scale RPCs