欧几里得空间和非欧空间
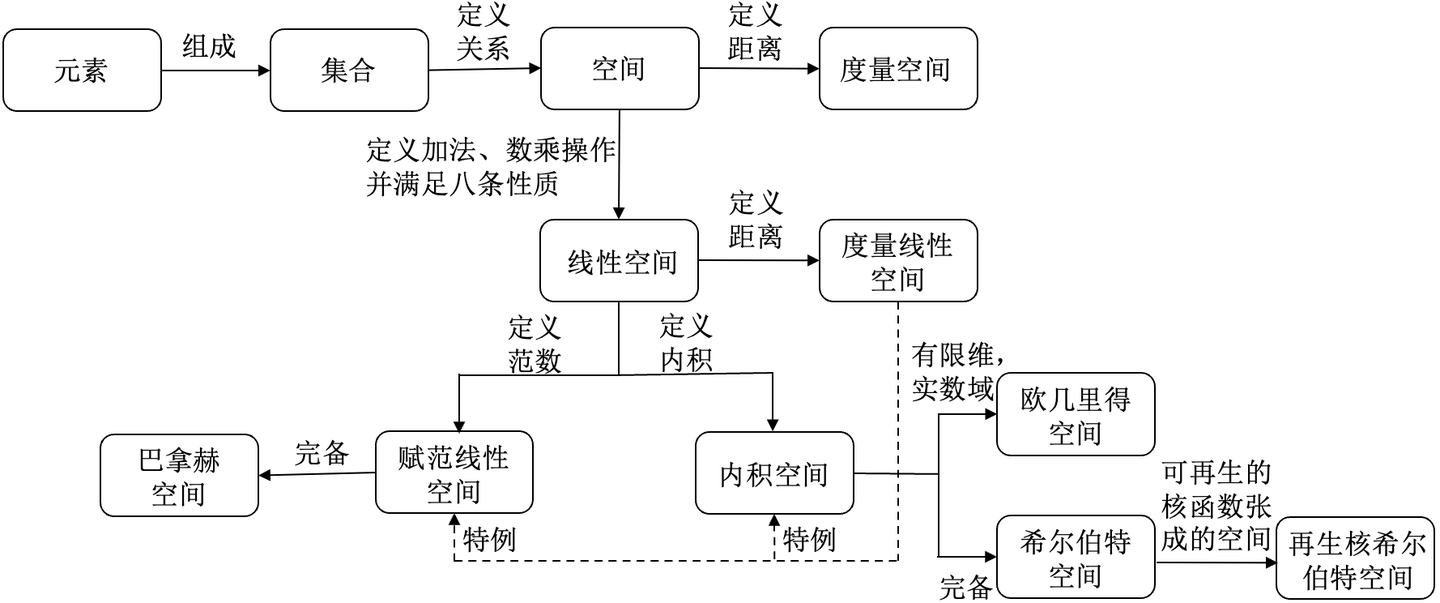
欧几里得空间
- 欧几里得空间就是在对现实空间的规则抽象和推广(从n<=3推广到有限n维空间)。
- 欧几里得几何就是中学学的平面几何、立体几何,在欧几里得几何中,平行线任何位置的间距相等。而中学学的几何空间一般是2维,3维(所以,我们讨论余弦值、点间的距离、内积都是在低纬空间总结的),如果将这些低维空间所总结的规律推广到有限的n维空间,那这些符合定义的空间则被统称为欧几里得空间(欧式空间,Euclidean Space)。
而欧几里得空间主要是定义了内积、距离、角(没错,就是初中的那些定义),理解了这些再去理解数学定义就很明确了。
非欧几里得空间
关于非欧式空间:非欧几何,爱因斯坦曾经形象地说明过:假定存在一种二维扁平智能生物,但它们不是生活在绝对的平面上,而是生活在一个球面上,那么,当它们在小范围研究圆周率的时候,会跟我们一样发现圆周率是3.14159……可是,如果它们画一个很大的圆,去测量圆的周长和半径,就会发现周长小于2πr,圆越大,周长比2πr小得越多,为了能够适用于大范围的研究,它们就必须修正它们的几何方法。如果空间有四维,而我们生活在三维空间中,而这个三维空间在空间的第四个维度中发生了弯曲,我们的几何就会象那个球面上的扁平智能生物一样,感受不到第四维的存在,但我们的几何必须进行修正,这就是非欧几何。在非欧几何中,平行的直线只在局部平行,就象地球的经线只在赤道上平行。闵可夫斯基空间属于欧几里得几何的扩展,它是把时间也作为一个维度进行量化,再添加光速系数,跟洛伦兹变换一样,使得不同惯性系中的运动问题计算得以简化。
欧几里得数据与非欧几里得数据
欧几里得数据
特点:“排列整齐”,是一类具有很好的平移不变性的数据。
图像中的平移不变性:即不管图像中的目标被移动到图片的哪个位置,得到的结果(标签)应该相同的。
对于这类数据以其中一个像素为中心点,其邻居节点的数量相同。可以很好的定义一个全局共享的卷积核来提取图像中相同的结构。常见这类数据有图像、文本、语言。
-
图像:图像是一种 2D的网格类型数据,通常用矩阵进行存储。
-
文本:文本是一种 1D 的网格类型数据,通常可以用向量进行存储。对于文本,我们通常做法是去停用词、以及高频词(DIFT),最后嵌入到一个一维的向量空间
非欧几里得数据
它是一类不具有平移不变性的数据。这类数据以其中的一个为节点,其邻居节点的数量可能不同。常见这类数据有知识图谱、社交网络、化学分子结构等等。
- 非欧几里德结构的样本总得来说有两大类型,分别是图(Graph)数据和流形数据( manifolds)
这两类数据有个特点就是,排列不整齐,比较的随意。
具体体现在:对于数据中的某个点,难以定义出其邻居节点出来,或者是不同节点的邻居节点的数量是不同的,这个其实是一个特别麻烦的问题,因为这样就意味着难以在这类型的数据上定义出和图像等数据上相同的卷积操作出来,而且因为每个样本的节点排列可能都不同,比如在生物医学中的分子筛选中,显然这个是一个Graph数据的应用,但是我们都明白,不同的分子结构的原子连接数量,方式可能都是不同的,因此难以定义出其欧几里德距离出来,这个是和我们的欧几里德结构数据明显不同的。因此这类型的数据不能看成是在欧几里德样本空间中的一个样本点了,而是要想办法将其嵌入(embed)到合适的欧几里德空间后再进行度量。而我们现在流行的 Graph Neural Network 便可以进行这类型的操作。这就是我们的后话了。
- 另外,欧几里德结构数据所谓的“排列整齐”也可以视为是一种特殊的非欧几里德结构数据,比如说是一种特殊的Graph数


