系统性能量化分析-6-课堂分享-Spark性能评估

https://journalofbigdata.springeropen.com/articles/10.1186/s40537-021-00499-7

用于 Hadoop 集群上 Spark 大数据作业性能表征的并行化模型

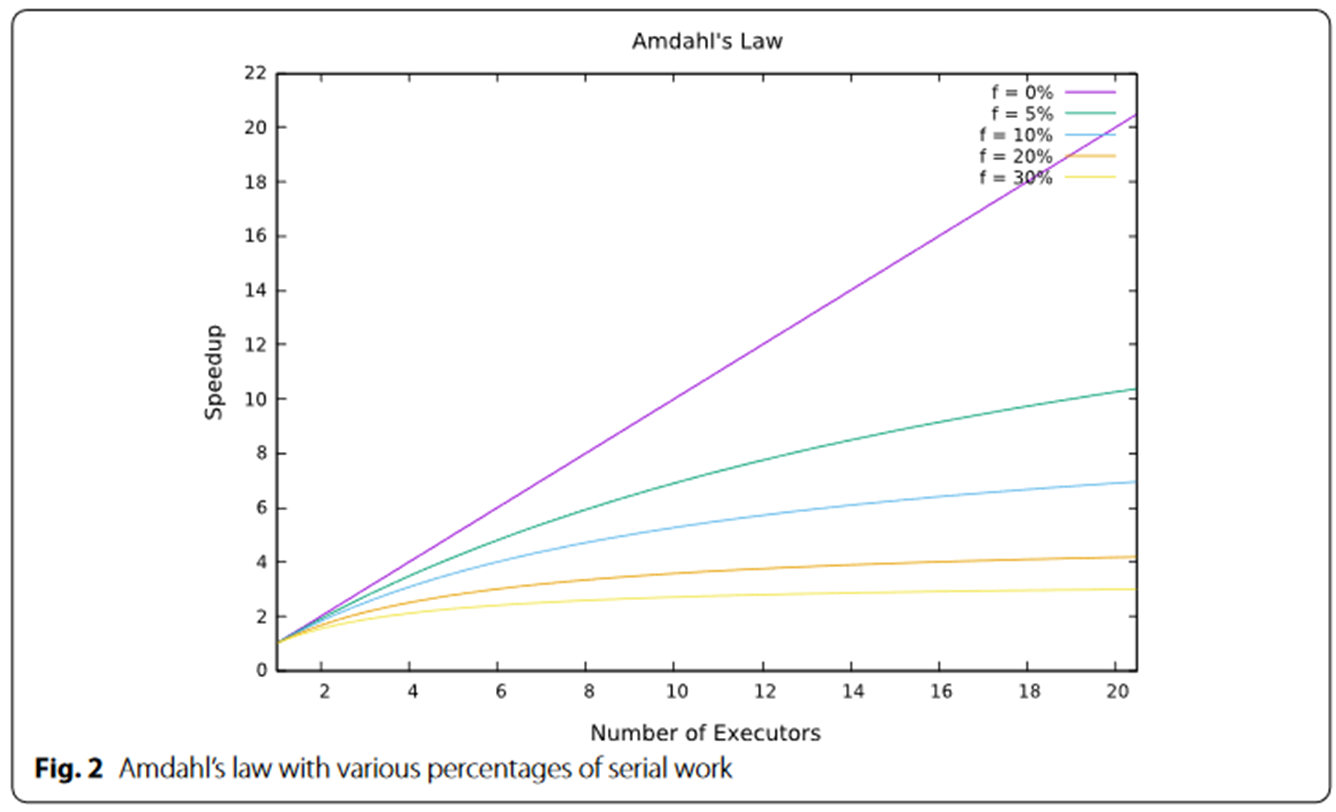
Amdahl’s Law

衡量：提升一个系统的一个部分的性能对整个系统有多大影响？

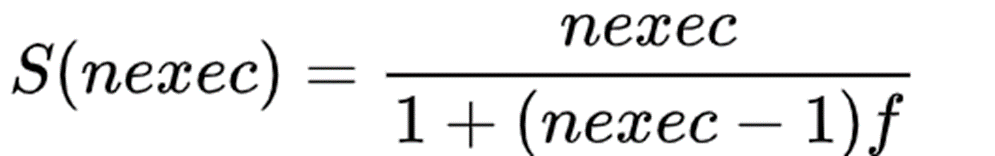
image-20231117105740479

  • 对于多内核系统或者分布式系统系统
    nexec 是处理器（或执行器）的数量， f 是串行作业百分比

  • 加速比上限： 1f\frac1{f}

image-20231117105810624

考虑到单个处理器运行某个工作负载需要时间 t，在多个处理器上运行的预测运行时为

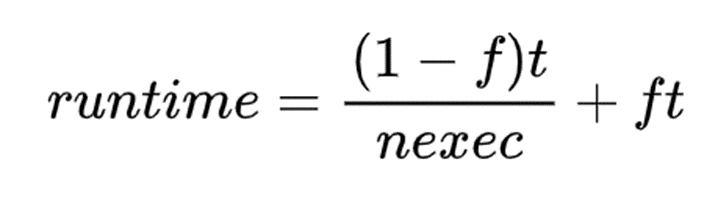
image-20231117105846630

加速比上限 1f\frac1{f}

处理时间下限是 ft, 由串行部分决定

运行时间 会随着executors的增加而急剧减少，

到达一定程度，再增加并行节点数的性价比

就会很低

也即大规模并行化，似乎是不可行的 ？？

image-20231117105925180

Gustafson’s law

[1] GUSTAFSON J L. Reevaluating Amdahl’s law[J/OL]. Communications of the ACM, 1988, 31(5): 532-533. DOI:10.1145/42411.42415.

  • 阿姆达定律：在问题确定的情况下，如何做性能加速，

  • 工程实践中：更多的是通过性能优化使得一个系统在问题规模可变的情况下，使得运行时间相对固定

  • 假设：
    程序的并行部分会随着问题规模的增加而增加。
    程序加载、串行瓶颈和 I/O 等构成运行 串行s 部分的时间不会随着问题规模的增大而增加。

这篇论文认为 阿姆达尔加速公式会给对大规模并行化 带来"心理障碍"；加速的衡量标准应该是问题与处理器数量的比例，而不是固定的问题大小。

所以提出了 古斯塔夫森定律

image-20231117110012026

N 是处理器的数量，
s 是串行处理时间，
p 是花在程序可并行部分上的时间

s+p = 1

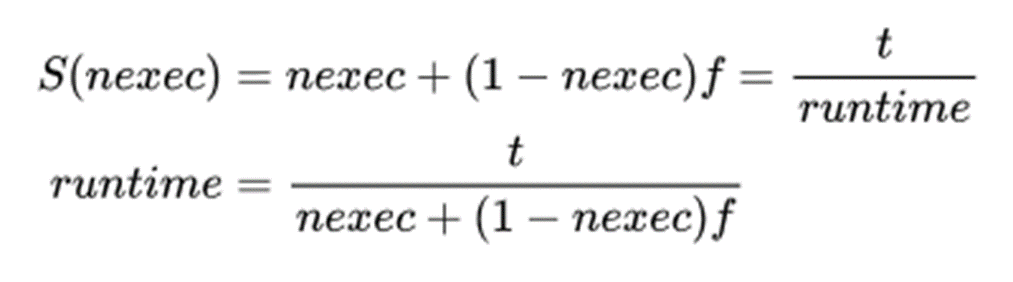
image-20231117110022776

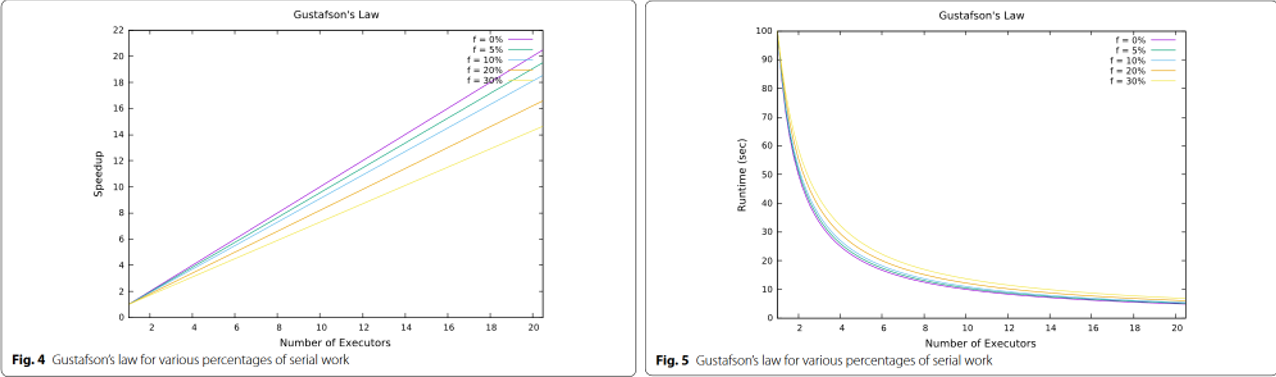
image-20231117110207057

这里加速比S单调递增，当然实际是不可能，

问题在于前提假设中，程序的串行部分，也是会随着问题规模，和并行节点数量的变化而变化

用于 Hadoop 集群上 Spark 大数据作业性能表征的并行化模型

https://journalofbigdata.springeropen.com/articles/10.1186/s40537-021-00499-7

用于 Hadoop 集群上 Spark 大数据作业性能表征的并行化模型

Spark 由主节点和工作节点组成
有很多可调控的参数:工作节点数，核数，分配内存数，缓存大小等等
这里主要考虑并行优化，考虑节点数

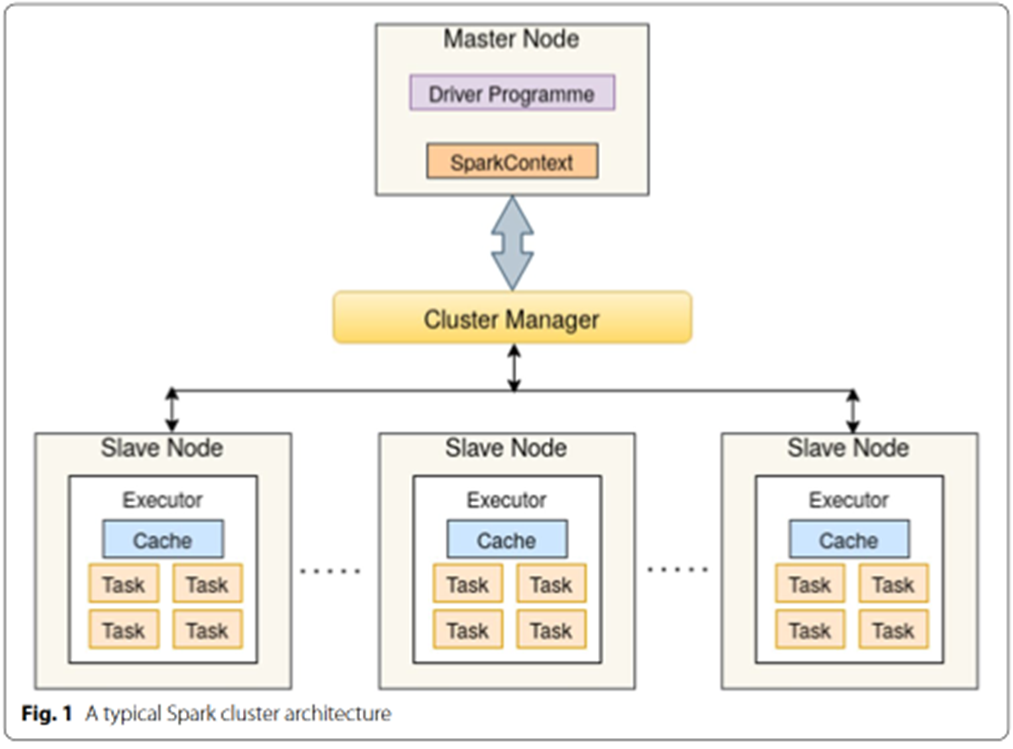
image-20231117110308295

现有性能模型不能解释

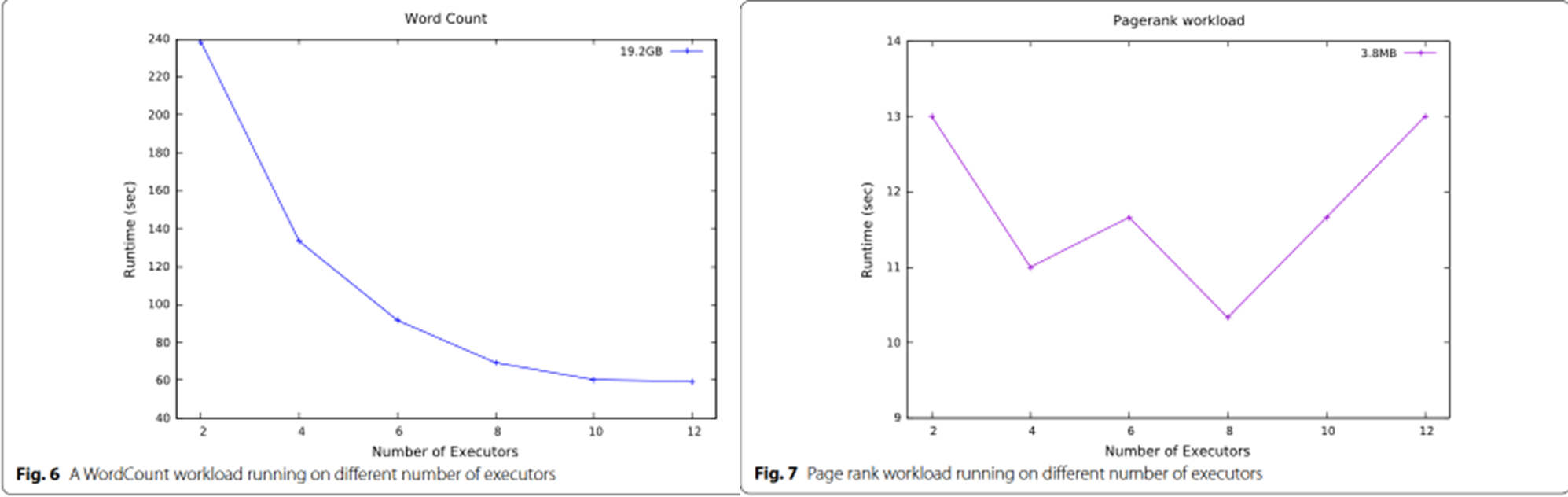
image-20231117110335332

从这里可以看到不同负载，

左边还可以用 阿姆达定律和古斯塔夫森定律解释，右边这个就没法解释了

区别在于工作负载的不同

PageRank 不同执行节点之间的通信和IO需求比 wordCount要多

构建新的评估模型

t 是在单个执行器中运行应用程序的时间，(可并行部分)
nexec 是执行器的数量，
t_serial 是在执行节点之间 I/O 、通信所需的额外时间.

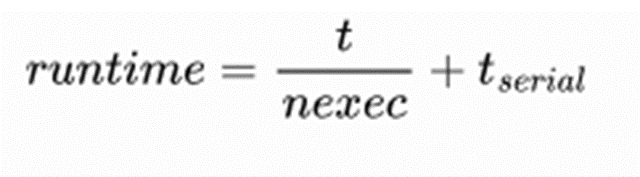
image-20231117110435451

公式关键是 tserial。在不了解应用程序内部算法实现的情况下，很难对其进行正确建模。

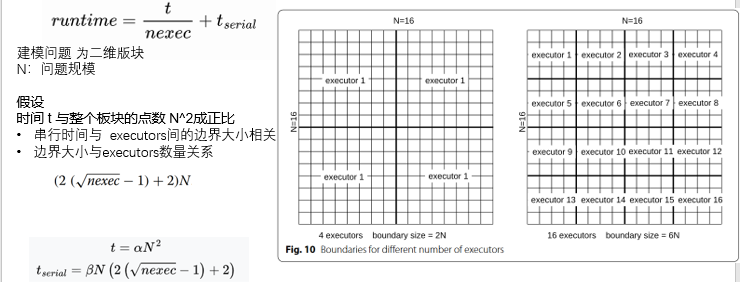
image-20231117110503589

公式简化分析

image-20231117110524136

实际，

a=f(N) ，表示并行部分执行时间，类似于问题算法的时间复杂度

b=g(N)，决定任务使用多个执行节点时，不同规模数据通信需求的增长情况

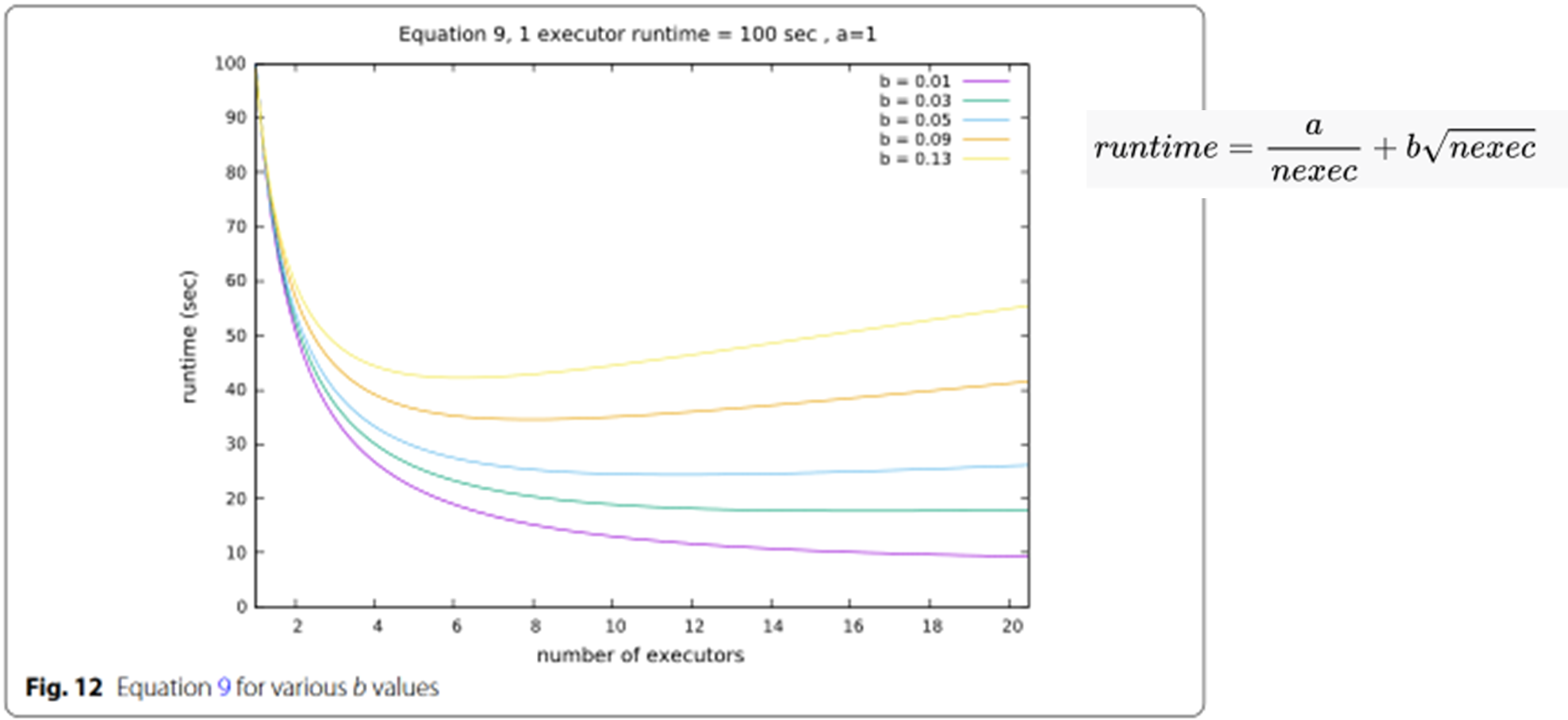
image-20231117110537298

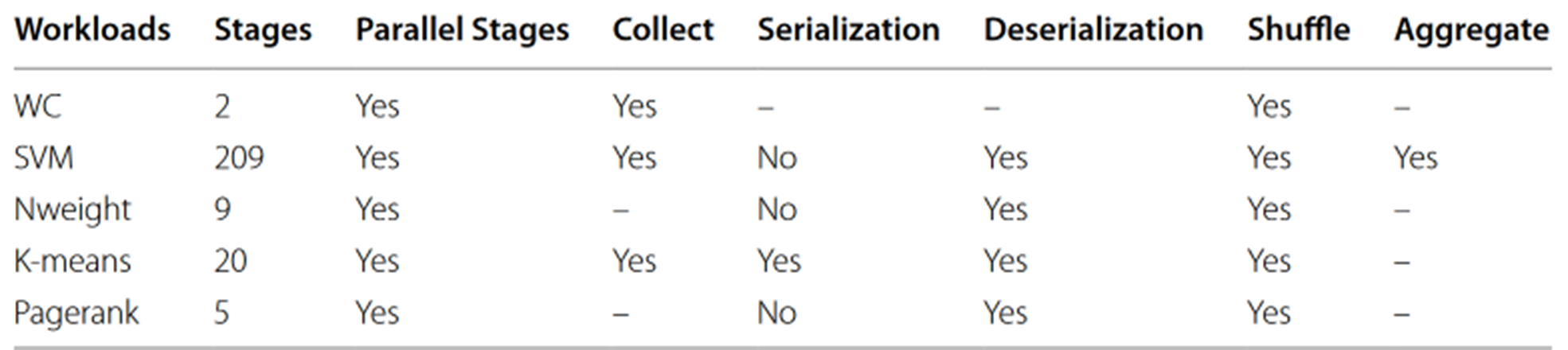
负载实验

image-20231117110634192

1. 模型拟合较好

这三个负载

wordcount, Nweight， SVM

在 SVM 的情况下（图 16），模型的拟合效果很好，它显示出性能在执行器数量达到一定数量时达到峰值。这正是模型所能解释的情况

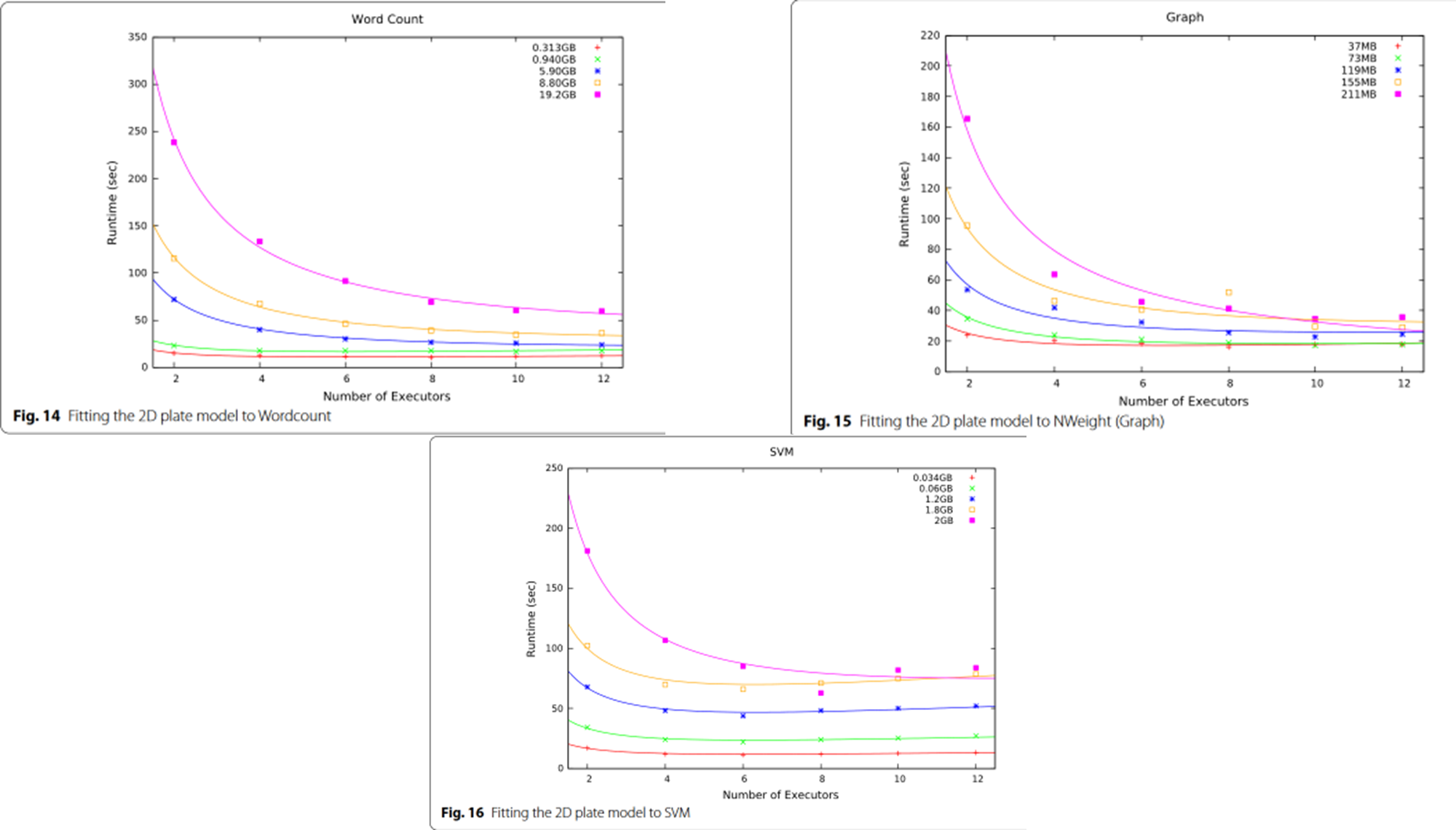
image-20231117110648525

模型拟合较差

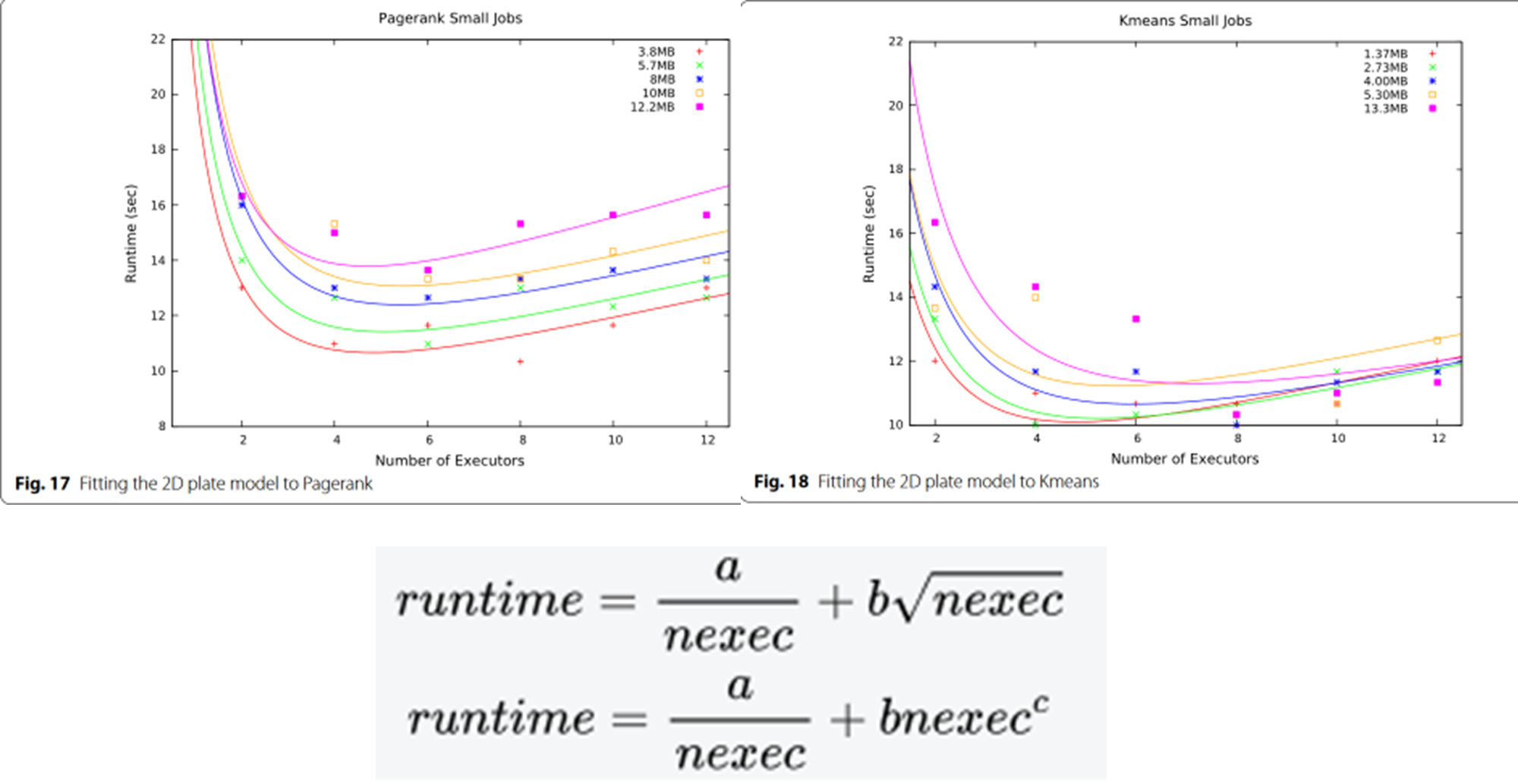
对于 Pagerank 和 Kmeans 这两种工作负载，模型的拟合效果并不理想（图 17 和 18）。当规模太小、运行时间相对较短时就会出现这种情况

在前面的工作中，边界的增长速度与 nexec 的平方根成正比。然后，我们将该函数调整为不同的指数，使其成为：

公式 9 是公式 11 的特例，其中 c = 0.5

image-20231117110726851

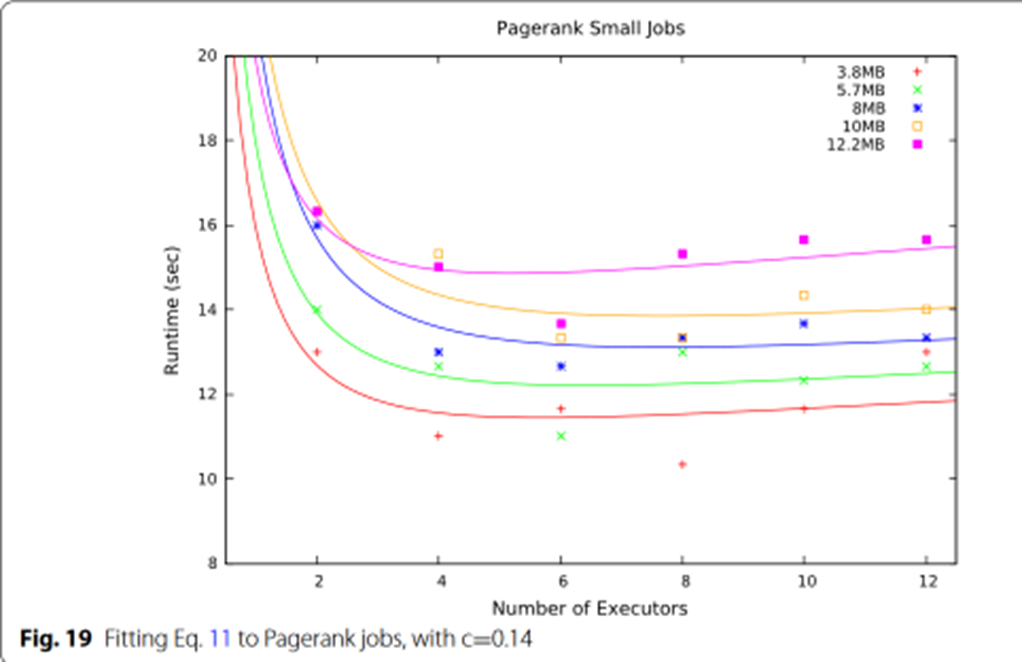
在通过 Gnuplot [35] 对公式 11 进行拟合后，我们发现当 c = 0.14 时，图 17 中使用的数据拟合得更为精确

这表明指数函数可以解释我们在这项工作中所针对的 建模并行节点数跟运行时关系

即运行时间在执行器达到一定数量时达到性能峰值，然后运行时间不断增长，即使增加更多执行器来运行作业，性能也会下降

image-20231117110812350

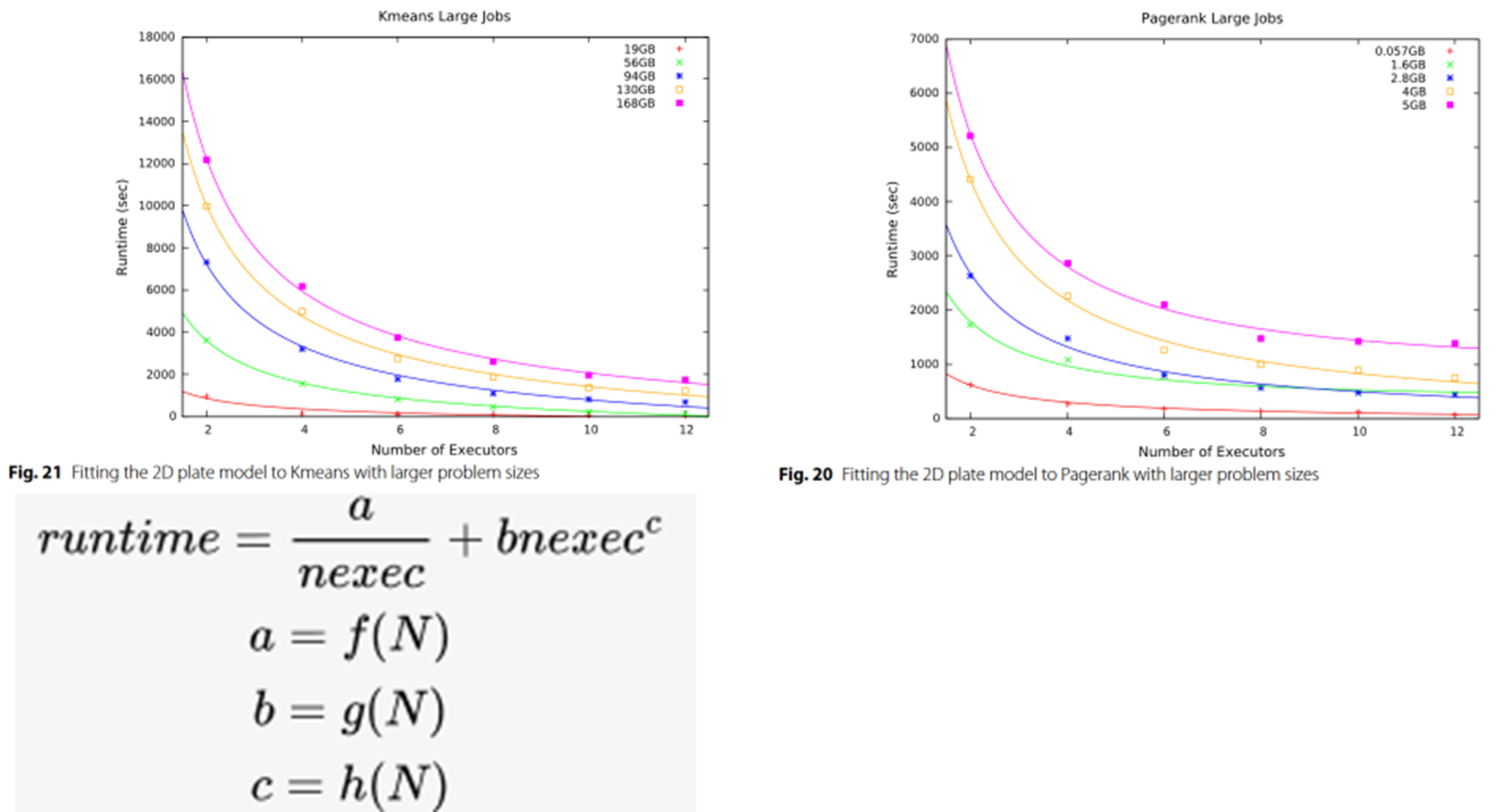
问题规模对模型参数的影响

对于更大的问题规模，Pagerank 与原始公式 非常吻合（图 20）。

Kmeans 也显示出与公式 更好的拟合（图 21）。这表明，串行部分与问题规模之间的关系也会发生变化。

image-20231117110906353

就 Pagerank 和 Kmeans 而言，常数 c 会随着问题规模的变化而变化。这是因为，当问题规模太小、作业运行时间只有几秒钟时，不可预测的开销可能会掩盖运行时间的模式。而较长的作业则更为稳定，更容易发现边界（串行部分）的增长模式。其他工作负载需要做更多工作

comparison with Amdahl’s and Gustafson’s laws

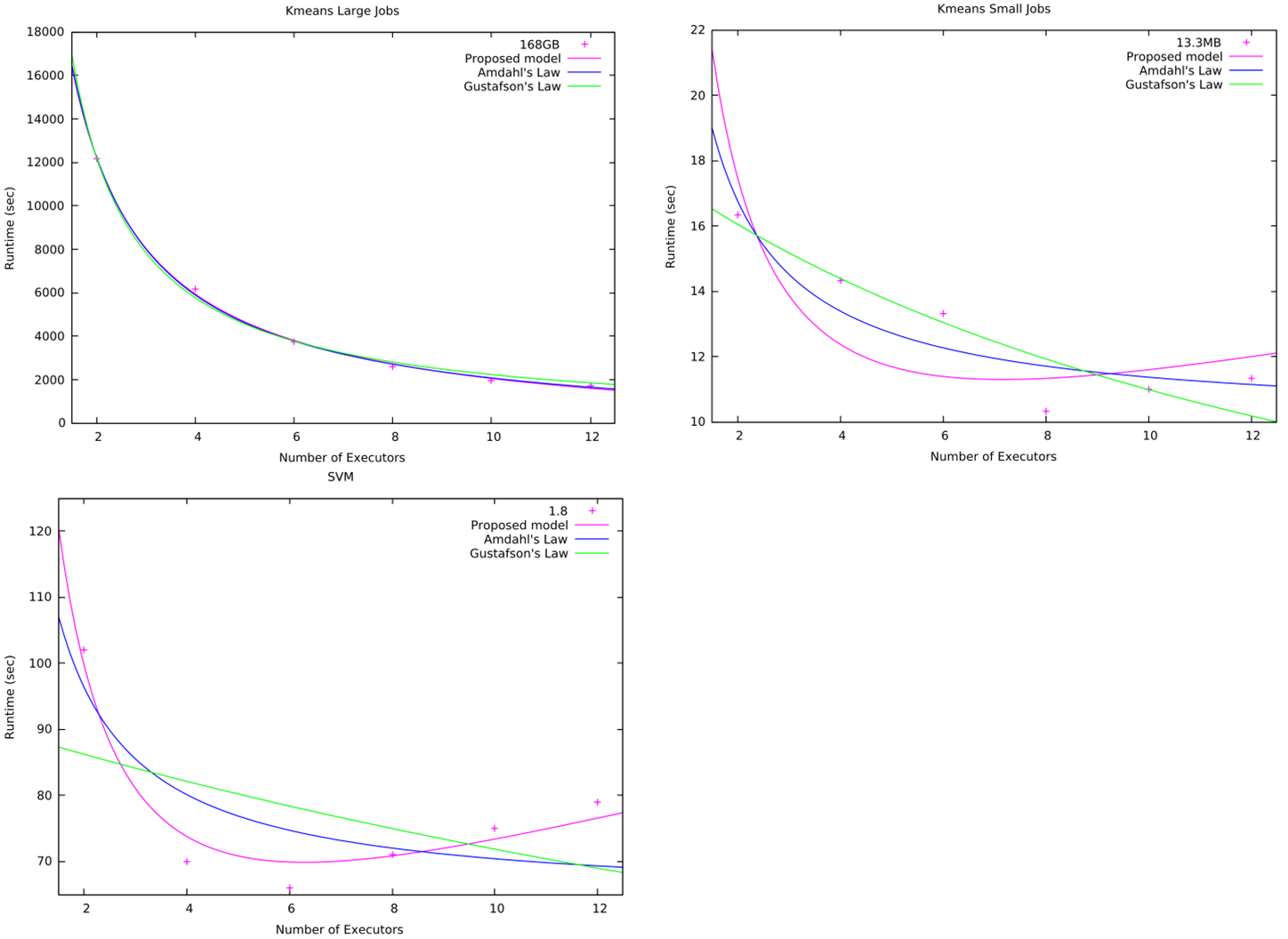
  • 在运行时间随执行器增加而下降再上升的负载中，我们的模型比 Amdahl 模型或 Gustafson 模型更有效。

  • 对于运行时间持续下降直到收敛到一个固定值的情况，三种模型都可能有效

image-20231117110925561

总结

  • 针对在 Hadoop 集群上运行的 Spark 大数据应用程序的不同工作负载提出了一种新的并行化模型。所提出的模型可以预测通用工作负载的运行时间与执行器数量的函数关系，而无需知道算法是如何实现的，只需通过相对较少的实验来确定模型方程的参数。
  • 进一步，在通过实验来确定模型方程参数的时候，可以考虑 同时考虑节点数和负载特征

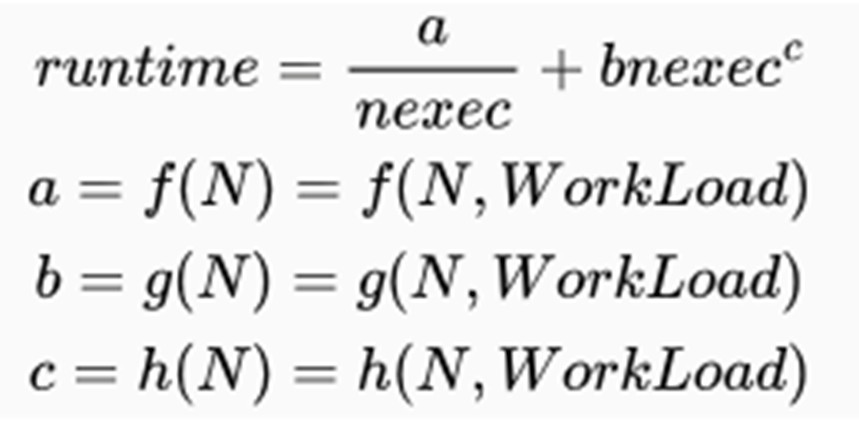
image-20231117111001056

reference

[1] GUSTAFSON J L. Reevaluating Amdahl’s law[J/OL]. Communications of the ACM, 1988, 31(5): 532-533. DOI:10.1145/42411.42415.

[2] AHMED N, BARCZAK A L C, RASHID M A, 等. A parallelization model for performance characterization of Spark Big Data jobs on Hadoop clusters[J/OL]. Journal of Big Data, 2021, 8(1): 107. DOI:10.1186/s40537-021-00499-7.

[3] DEB D. Gnuplot Helper – a new Utility for gnuplot Graph Plotting Software[R/OL]. In Review, 2021[2023-11-14]. https://www.researchsquare.com/article/rs-548261/v1. DOI:10.21203/rs.3.rs-548261/v1.