传统排序方法

  1. 传统的排序方法通过构造相关度函数，按照相关度进行排序。
    很难融合多种因数，比如向量空间模型以tf*idf作为权重构建相关度函数，就很难利用其他信息了，
  2. 并且如果模型中参数比较多，也会使得调参非常困难，而且很可能会出现过拟合现象。

Ranking模型可以粗略分为基于相关度和机遇重要性进行排序。

基于相关度的模型，通常利用query和doc之间的词共现特性（如布尔模型）、VSM（如TFIDF、LSI等）、概率排序思想（BM25、LMIR）等。

基于重要性的模型，利用的是doc本身的重要性，如pageRank、TructRank等。

Learning To Rank

LTR（Learning to rank）是一种==监督学习==（SupervisedLearning）的==排序方法==，已经被广泛应用到推荐与搜索等领域。

LTR采用机器学习

很好地解决了这一问题。机器学习方法很容易融合多种特征，而且有成熟深厚的理论基础，并有一套成熟理论解决稀疏、过拟合等问题。

排序学习方法分为PointWise、PairWise、ListWise三种不同的方式，参考《A Short Introduction to Learning to Rank》

三种方法并不是特定的算法，而是排序学习模型的设计思路，主要区别体现在损失函数（Loss Function）、以及相应的标签标注方式和优化方法的不同。

LTR中单文档方法是将训练集里每一个文档当做一个训练实例,文档对方法是将同一个查询的搜索结果里任意两个文档对作为一个训练实例,文档列方法是将一个查询里的所有搜索结果列表作为一个训练实例.

  • 设q 为query，D(d_i,…… d_n) 为返回的文档对，如何排序

    1. Point-Wise: $$F(d_i) = Y_{qi}$$ 根据相关度Y 对D排序
    2. Pair-Wise : $$F(q,(d_i,d_j))$$ ； 二分类，确定d_i,和d_j的顺序关系
    3. List-Wise: $$F(q,D) = Y_{D}$$ ；(q,D)相对于尝试学习每一个样本是否相关或者两个文档的相对比较关系，列表法排序学习的基本思路是尝试直接优化像 NDCG（Normalized Discounted Cumulative Gain）这样的指标，从而能够学习到最佳排序结果

img

PointWise 单点法

Pointwise方法是这三种排序学习方法中最简单点一种，它是思想是直接将排序问题转换成了分类或者回归问题

假如已有排序学习的训练数据集，每个query对应了多个不同的多doc，并且每个doc与相应query的相关度已知道，那么Pointwise方法在训练时会把每个单独的doc本身看作X ，把与query的相关度看作Y ，然后利用分类或者回归模型进行训练，最后依据利用训练好的模型对不同doc的打分进行排序

p

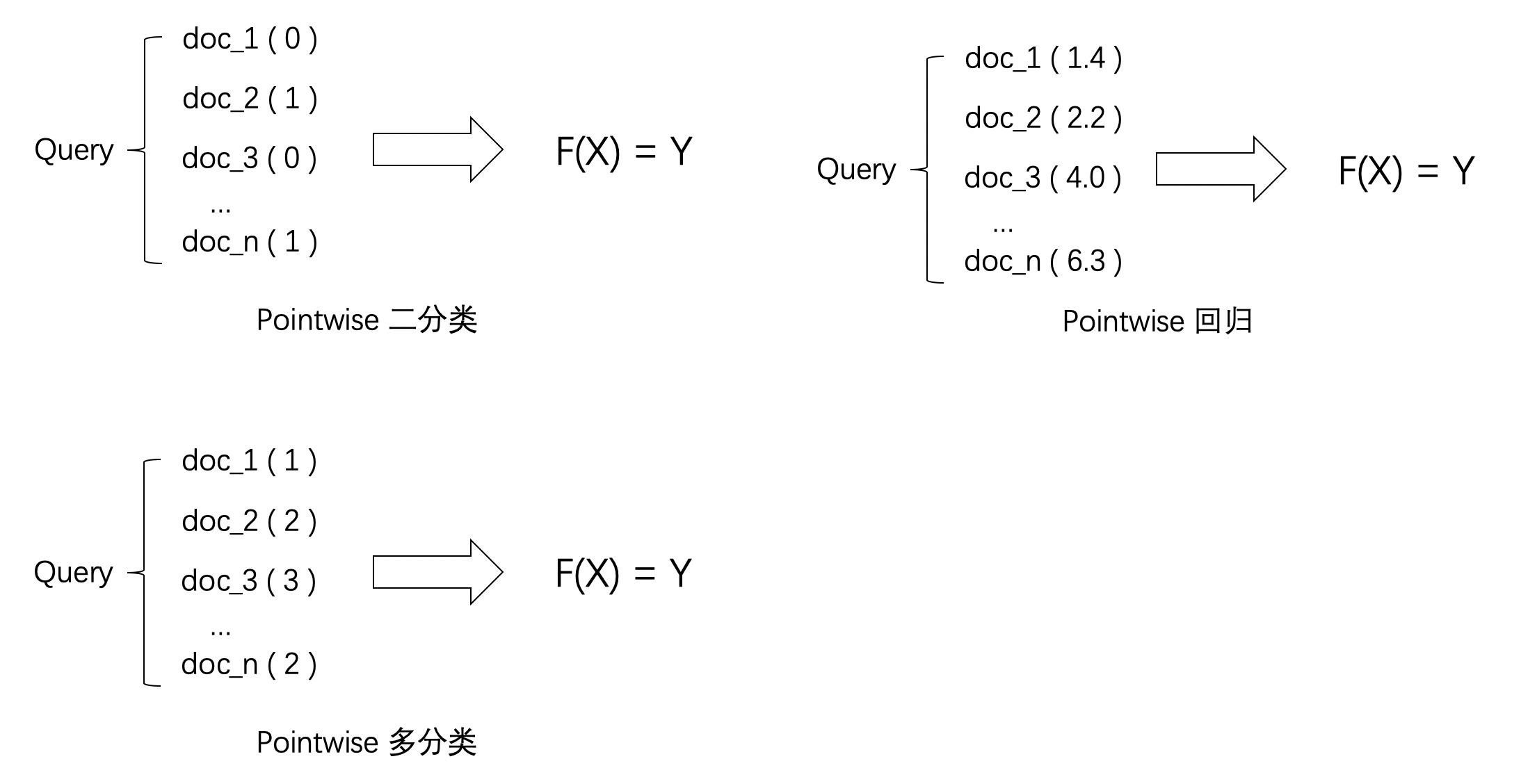
0/1变量 时，为PosintWise二分类

为离散变量时，为PointWise多分类

为连续变量时，为PointWise回归

PointWise 方法存在的问题：

PointWise 方法通过优化损失函数求解最优的参数，可以看到 PointWise 方法非常简单，工程上也易实现，但是 PointWise 也存在很多问题：

  1. PointWise ==只考虑单个文档同 query 的相关性==，没有考虑文档间的关系，即假设各个doc之间是相互独立的，这种假设是不成立的。
    然而排序追求的是排序结果，并不要求精确打分，只要有相对打分即可；
  2. 通过分类只是把不同的文档做了一个简单的区分，同一个类别里的文档则无法深入区别，虽然我们可以根据预测的概率来区别，但实际上，==这个概率只是准确度概率，并不是真正的排序靠前的预测概率==；
  3. PointWise 方法并没有考虑同一个 query 对应的文档间的内部依赖性。
    • 一方面，导致输入空间内的样本不是 IID 的，违反了 ML 的基本假设，
    • 另一方面，没有充分利用这种样本间的结构性。
    • 其次，当不同 query 对应不同数量的文档时，==整体 loss 将容易被对应文档数量大的 query 组所支配==，应该每组 query 都是等价的才合理。
  4. 很多时候，排序结果的 Top N 条的顺序重要性远比剩下全部顺序重要性要高，==因为损失函数没有相对排序位置信息，这样会使损失函数可能无意的过多强调那些不重要的 docs，==即那些排序在后面对用户体验影响小的 doc，所以对于位置靠前但是排序错误的文档应该加大惩罚。

数据输入和输出形式：

Pointwise方法是通过近似为回归问题解决排序问题，

  1. 输入的单条样本为得分-文档，将每个查询-文档对的相关性得分作为实数分数或者序数分数，使得单个查询-文档对作为样本点(Pointwise的由来)，训练排序模型。

  2. 预测时候对于指定输入，给出查询-文档对的相关性得分。

  • 代表算法：

基于神经网络的排序算法 RankProp、基于感知机的在线排序算法 Prank(Perception Rank)/OAP-BPM 和基于 SVM 的排序算法。

推荐中使用较多的 Pointwise 方法是 LR、GBDT、SVM、FM 以及结合 DNN 的各种排序算法。

PairWise 配对法

配对法的基本思路是对样本进行两两比较，构建偏序文档对，从比较中学习排序，因为对于一个查询关键字来说，最重要的其实不是针对某一个文档的相关性是否估计得准确，而是要能够正确估计一组文档之间的 “相对关系”。

PairWise方法的思想是将同一个query下多个不同doc之间进行两两组对，然后将<doc, doc>pair doc作为模型输入进行一个二分类的任务学习。PairWise首先将doc进行两两组对，然后比较doc与query的相关度大小，如果第一个doc的相关度大于第二个doc，则这对doc的标签设置为1否则为0。常用模型包括有RankNet、LambdaRank、LambdaMart等。

因此，Pairwise 的训练集样本从每一个 “关键字文档对” 变成了 “关键字文档文档配对”。也就是说，每一个数据样本其实是一个比较关系，当前一个文档比后一个文档相关排序更靠前的话，就是正例，否则便是负例，如下图。试想，有三个文档：A、B 和 C。完美的排序是 “B>C>A”。我们希望通过学习两两关系 “B>C”、“B>A” 和 “C>A” 来重构 “B>C>A”。

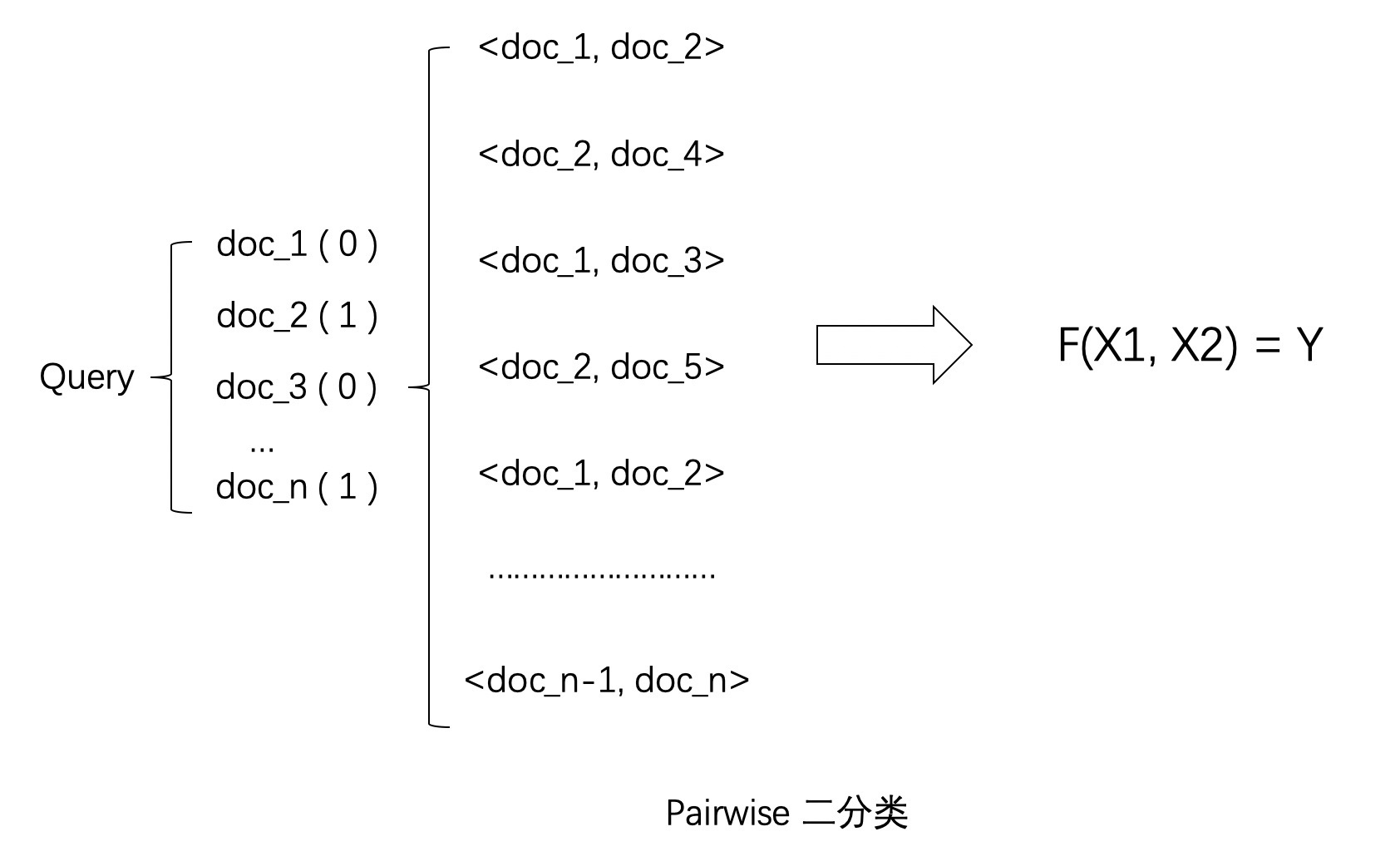
v2-3f03a6e52527d5992482cc3e3f075650_r

这里面有几个非常关键的假设。换句话说，标注是一个困难的事情，难点在于：是否存能得到完美关系？是否能重构完美排序？

Pairwise 方法存在的问题：

Pairwise 方法通过考虑两两文档之间的相关对顺序来进行排序，相比 PointWise 方法有明显改善。但 Pairwise 方法仍有如下问题：

  1. 使用的==是两文档之间相关度的损失函数，而它和真正衡量排序效果的指标之间存在很大不同==，甚至可能是负相关的，如可能出现 Pairwise Loss 越来越低，但 NDCG 分数也越来越低的现象。
  2. ==只考虑了两个文档的先后顺序，且没有考虑文档在搜索列表中出现的位置==，导致最终排序效果并不理想。
  3. ==不同的查询，其相关文档数量差异很大==，转换为文档对之后，有的查询可能有几百对文档，有的可能只有几十个，这样不加均一化地在一起学习，模型会优先考虑文档对数量多的查询，减少这些查询的 loss，最终对机器学习的效果评价造成困难。
  4. Pairwise 方法的训练样例是偏序文档对，它将对文档的排序转化为对不同文档与查询相关性大小关系的预测；因此，如果因某个文档相关性被预测错误，或文档对的两个文档相关性均被预测错误，则会影响与之关联的其它文档，进而引起连锁反应并影响最终排序结果。

数据输入和输出形式：

Pairwise方法是通过近似为分类问题解决排序问题，输入的单条样本为标签-文档对。

  1. 对于一次查询的多个结果文档，组合任意两个文档形成文档对作为输入样本。即学习一个二分类器，对输入的一对文档对AB（Pairwise的由来），根据A相关性是否比B好，二分类器给出分类标签1或0。
  2. 对所有文档对进行分类，就可以得到一组偏序关系，从而构造文档全集的排序关系。
  3. 该类方法的原理是对给定的文档全集S，降低排序中的逆序文档对的个数来降低排序错误，从而达到优化排序结果的目的。
  • 代表算法：

基于 SVM 的 Ranking SVM 算法、基于神经网络的 RankNet 算法和基于 Boosting 的 RankBoost 算法。

ListWise 列表法

相对于尝试学习每一个样本是否相关或者两个文档的相对比较关系，列表法排序学习的基本思路是尝试直接优化像 NDCG（Normalized Discounted Cumulative Gain）这样的指标，从而能够学习到最佳排序结果。

列表法的相关研究有很大一部分来自于微软研究院，这其中著名的作者就有微软亚州院的徐君、李航、刘铁岩等人，以及来自微软西雅图的研究院的著名排序算法 LambdaMART 以及 Bing 搜索引擎的主导人克里斯托弗·博格斯（Christopher J.C. Burges）。

列表法排序学习有两种基本思路。

  1. 第一种称为 Measure-specific，就是直接针对 NDCG 这样的指标进行优化。
    目的简单明了，用什么做衡量标准，就优化什么目标。
  2. 第二种称为 Non-measure specific，则是根据一个已经知道的最优排序，尝试重建这个顺序，然后来衡量这中间的差异。

Measure-specific

先来看看直接优化排序指标的难点和核心在什么地方。

  • 难点在于，希望能够优化 NDCG 指标这样的 “理想” 很美好，但是现实却很残酷。
    NDCG、MAP 以及 AUC 这类排序标准，都是在数学的形式上的 “非连续”（Non-Continuous）和 “非可微分”（Non-Differentiable）。
    而绝大多数的优化算法都是基于 “连续”（Continuous）和 “可微分”（Differentiable）函数的。因此，直接优化难度比较大。

三种思路

  • 第一种方法是，既然直接优化有难度，那就找一个近似 NDCG 的另外一种指标。而这种替代的指标是 “连续” 和 “可微分” 的 。只要我们建立这个替代指标和 NDCG 之间的近似关系，那么就能够通过优化这个替代指标达到逼近优化 NDCG 的目的。这类的代表性算法的有 SoftRank 和 AppRank。

  • 第二种方法是，尝试从数学的形式上写出一个 NDCG 等指标的 “边界”（Bound），然后优化这个边界。比如，如果推导出一个上界，那就可以通过最小化这个上界来优化 NDCG。这类的代表性算法有 SVM-MAP 和 SVM-NDCG。

  • 第三种方法则是，希望从优化算法上下手，看是否能够设计出复杂的优化算法来达到优化 NDCG 等指标的目的。对于这类算法来说，算法要求的目标函数可以是 “非连续” 和 “非可微分” 的。这类的代表性算法有 AdaRank 和 RankGP

Non-measure specific

这种思路的主要假设是，已经知道了针对某个搜索关键字的完美排序，那么怎么通过学习算法来逼近这个完美排序。我们希望缩小预测排序和完美排序之间的差距。值得注意的是，在这种思路的讨论中，优化 NDCG 等排序的指标并不是主要目的。这里面的代表有 ListNet 和 ListMLE。

  • Listwise 方法存在的问题：

    列表法相较单点法和配对法针对排序问题的模型设计更加自然，解决了排序应该基于 query 和 position 问题。

    但列表法也存在一些问题：一些算法需要基于排列来计算 loss，从而使得训练复杂度较高，如 ListNet 和 BoltzRank。此外，位置信息并没有在 loss 中得到充分利用，可以考虑在 ListNet 和 ListMLE 的 loss 中引入位置折扣因子

  • 基于列的学习排序(Listwise Approach)是将qid=10对应的所有查询文档作为一个实例进行训练,即一个查询及其对应的所有搜索结果评分作为一个实例进行训练;训练得到一个最后评分函数F后,test测试集中一个新的查询,函数F对每一个文档进行打分,之后按照得分顺序由高到低排序即是对应搜索的结果.

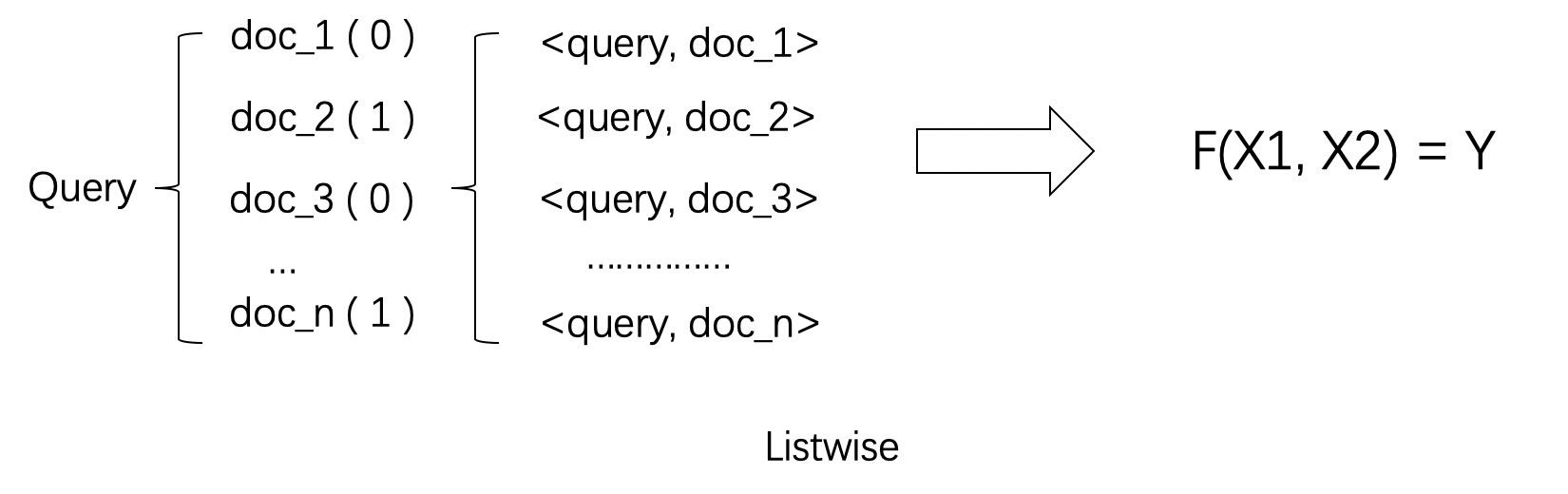
v2-0bc0cd36af20a0d781b49755368332ca_r

  • 代表算法：

基于 Measure-specific 的 SoftRank、SVM-MAP、SoftRank、LambdaRank、LambdaMART，基于 Non-measure specific 的 ListNet、ListMLE、BoltzRank。

推荐中使用较多的 Listwise 方法是 LambdaMART。

评价

ListWise方法相比于pariwise和pointwise往往更加直接，它专注于自己的目标和任务，直接对文档排序结果进行优化，因此往往效果也是最好的。

Point wise pairwise list wise
思想 Pointwise排序是将训练集中的每个item看作一个样本获取rank函数，主要解决方法是把分类问题转换为单个item的分类或回归问题。 Pairwise排序是将同一个查询中两个不同的item作为一个样本，主要思想是把rank问题转换为二值分类问题 Listwise排序是将整个item序列看作一个样本，通过直接优化信息检索的评价方法和定义损失函数两种方法实现。
算法 1、基于回归的算法；
2、基于分类的算法；
3、基于有序回归的算法		 基于二分类的算法 直接基于评价指标的算法
非直接基于评价指标的算法
缺点 ranking 追求的是排序结果，并不要求精确打分，只要有相对打分即可。
pointwise 类方法并没有考虑同一个 query 对应的 docs 间的内部依赖性。一方面，导致输入空间内的样本不是 IID 的，违反了 ML 的基本假设，另一方面，没有充分利用这种样本间的结构性。
其次，当不同 query 对应不同数量的 docs 时，整体 loss 将会被对应 docs 数量大的 query 组所支配，前面说过应该每组 query 都是等价的。损失函数也没有 model 到预测排序中的位置信息。因此，损失函数可能无意的过多强调那些不重要的 docs，即那些排序在后面对用户体验影响小的 doc。		 1、如果人工标注包含多有序类别，那么转化成 pairwise preference 时必定会损失掉一些更细粒度的相关度标注信息。
2、doc pair 的数量将是 doc 数量的二次，从而 pointwise 类方法就存在的 query 间 doc 数量的不平衡性将在 pairwise 类方法中进一步放大。
3、pairwise 类方法相对 pointwise 类方法对噪声标注更敏感，即一个错误标注会引起多个 doc pair 标注错误。
4、pairwise 类方法仅考虑了 doc pair 的相对位置，损失函数还是没有 model 到预测排序中的位置信息。
5、pairwise 类方法也没有考虑同一个 query 对应的 doc pair 间的内部依赖性，即输入空间内的样本并不是 IID 的，违反了 ML 的基本假设，并且也没有充分利用这种样本间的结构性。		 listwise 类相较 pointwise、pairwise 对 ranking 的 model 更自然，解决了 ranking 应该基于 query 和 position 问题。
listwise 类存在的主要缺陷是：
一些 ranking 算法需要基于排列来计算 loss，从而使得训练复杂度较高，如 ListNet和 BoltzRank。
此外，位置信息并没有在 loss 中得到充分利用，可以考虑在 ListNet 和 ListMLE 的 loss 中引入位置折扣因子。
优点 1、输入空间中样本是单个 doc（和对应 query）构成的特征向量；
2、输出空间中样本是单个 doc（和对应 query）的相关度；
3、假设空间中样本是打分函数；损失函数评估单个 doc 的预测得分和真实得分之间差异。		 输入空间中样本是（同一 query 对应的）两个 doc（和对应 query）构成的两个特征向量；
输出空间中样本是 pairwise preference；假设空间中样本是二变量函数；损失函数评估 doc pair 的预测 preference 和真实 preference 之间差异。		 输入空间中样本是（同一 query 对应的）所有 doc（与对应的 query）构成的多个特征向量（列表）；
输出空间中样本是这些 doc（和对应 query）的相关度排序列表或者排列；
假设空间中样本是多变量函数，对于 docs 得到其排列，实践中，通常是一个打分函数，根据打分函数对所有 docs 的打分进行排序得到 docs 相关度的排列；损失函数分成两类，一类是直接和评价指标相关的，还有一类不是直接相关的。

参考

  • 转载
  1. Learning to Rank： pointwise 、 pairwise 、 listwise
  2. Introduction to Learning-to-Rank
  3. 【推荐】pairwise、pointwise 、 listwise算法是什么?怎么…
  4. 排序学习-2.排序学习方法分类 - 知乎 (zhihu.com)
  5. 推荐- Point wise、pairwise及list wise的比较 - 知乎 (zhihu.com)